Keskeisen suuntauksen ihanteellinen mitta on sellainen, joka on selkeästi määritelty, helposti ymmärrettävä, yksinkertaisesti laskettavissa. Sen olisi perustuttava kaikkiin havaintoihin ja vähiten niihin, joita tietokokonaisuudessa esiintyvät äärimmäiset havainnot vaikuttavat.
Ihmiset usein vastustavat näitä kahta toimenpidettä, mutta tosiasia on, että ne ovat erilaisia. Tässä artikkelissa korostetaan erityisesti keskiarvon ja mediaanin välisiä eroja. Katso.
Vertailukaavio
| Vertailun perusteet | Tarkoittaa | Mediaani |
|---|---|---|
| merkitys | Keskiarvo viittaa tiettyjen arvojen tai määrien yksinkertaiseen keskiarvoon. | Median määritellään keskiarvoksi tilattujen arvojen luettelossa. |
| Mikä se on? | Se on aritmeettinen keskiarvo. | Se on sijainnin keskiarvo. |
| edustaa | Tietokokonaisuuden painopiste | Tietokokonaisuuden painopiste Tietokokonaisuuden keskipiste |
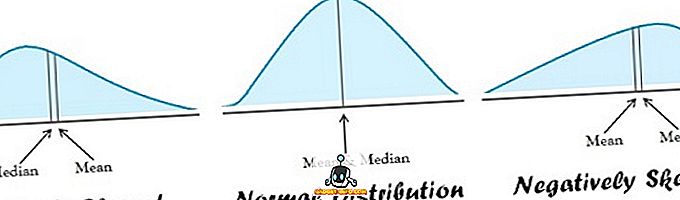
| sovellettavuus | Normaalijakauma | Kallistettu jakauma |
| poikkeavia havaintoja | Keskiarvo on herkkä ulkopuolisille. | Mediaani ei ole herkkä ulkopuolisille. |
| Laskeminen | Keskiarvo lasketaan lisäämällä kaikki havainnot ja jakamalla sitten saatu arvo havaintojen määrällä. | Keskiarvon laskemiseksi datajoukko on järjestetty nousevaan tai laskevaan järjestykseen, sitten arvo, joka laskee uuden tietosarjan keskelle, on mediaani. |
Määritelmä keskiarvo
Keskiarvo on laajasti käytetty keskeisen suuntauksen mittari, joka määritellään arvosarjan keskiarvoksi. Se edustaa tietyn arvomäärän mallia ja yleisintä arvoa. Se voidaan laskea sekä erillisissä että jatkuvissa sarjoissa.
Keskiarvo on kaikkien havaintojen summa jaettuna havainnon määrällä aineistossa. Jos muuttujan oletettu arvo on yhtä suuri, sen keskiarvo on sama. Keskiarvo voi olla kahdentyyppinen, näytteen keskiarvo (x̅) ja populaation keskiarvo (µ). Se voidaan laskea annetulla kaavalla:
- Aritmeettinen keskiarvo :

n = arvojen lukumäärä - Diskreettisarja :

- Jatkuville palveluksille :

A = Oletettu keskiarvo
C = Yhteinen jakaja
Määritelmä mediaani
Median on toinen tärkeä keskeisen suuntauksen mittari, jota käytetään jakamaan arvo kahteen yhtä suureen osaan eli suurempaan puoleen näytteestä, populaatiosta tai todennäköisyysjakaumasta alemmalta puolelta. Se on keskiarvoarvo, joka saavutetaan, kun havainnot lajitellaan tietyssä järjestyksessä, joko nousevassa tai laskevassa järjestyksessä.
Keskiarvon laskemiseen on ensin järjestettävä havainnot pienimmistä korkeimpiin tai korkeimpiin ja alimpiin, ja sitten sovellettava sopiva kaava, joka on alla olevien ehtojen mukaan:
- Jos havaintojen määrä on pariton :

- Jos havaintojen määrä on jopa :

- Jatkuville sarjoille :

c = edellisen mediaaniluokan kumulatiivinen taajuus
f = mediaaniluokan taajuus
h = luokan leveys
Keskiarvon ja keskiarvon väliset erot
Keskiarvon ja mediaanin väliset merkittävät erot esitetään seuraavassa artikkelissa:
- Tilastoissa keskiarvo määritellään annettujen arvojen tai määrien yksinkertaisena keskiarvona. Mediaanin sanotaan olevan keskiarvo tilattujen arvojen luettelossa.
- Vaikka keskiarvo on aritmeettinen keskiarvo, mediaani on sijaintikeskiarvo, olennaisesti dataryhmän sijainti määrää mediaanin arvon.
- Keskiarvo kuvaa datayksikön painopisteen, kun taas mediaani korostaa dataryhmän keskiarvoarvoa.
- Keskiarvo on sopiva normaalijakautuneille tiedoille. Toisaalta mediaani on paras, kun tiedonjako on vinossa.
- Keskiarvoon vaikuttaa voimakkaasti ääriarvo, joka ei ole mediaanilla.
- Keskiarvo lasketaan lisäämällä kaikki havainnot ja jakamalla sitten saatu arvo havaintojen lukumäärällä; tulos on keskiarvo. Toisin kuin mediaani, datajoukko on järjestetty nousevaan tai laskevaan järjestykseen, jolloin uuden dataryhmän keskiarvoon laskeva arvo on mediaani.
esimerkki
Etsi tietokokonaisuuden keskiarvo ja mediaani:
58, 26, 65, 34, 78, 44, 96
Ratkaisu: Keskiarvon laskemiseksi sinun on jaettava havaintojen summa havaintojen määrällä,

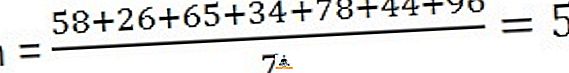
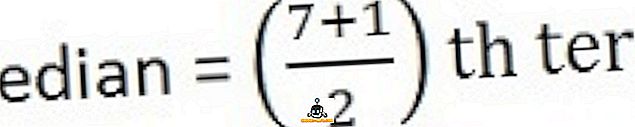
Voit laskea mediaanin ensin järjestämään sarjan sarjassa, eli alimmasta korkeimpaan,
26, 34, 44, 58, 65, 78, 96
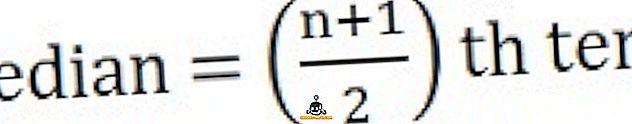
johtopäätös
Kun olet tarkastellut edellä mainittuja kohtia, voimme sanoa, että nämä kaksi matemaattista käsitettä ovat erilaisia. Aritmeettista keskiarvoa tai keskiarvoa pidetään keskeisenä suuntauksena parhaiten mitattuna, koska se sisältää kaikki ihanteellisen mittauksen piirteet, mutta sillä on yksi haittapuoli, että näytteenottovaihtelut vaikuttavat keskiarvoon.
Samalla tavalla mediaani määritellään myös yksiselitteisesti ja helposti ymmärrettäväksi ja laskettavaksi. Paras asia tässä mittakaavassa on se, että näytteenottomuutokset eivät vaikuta siihen, mutta mediaanin ainoa haitta on se, että se ei perustu kaikkiin havaintoja. Avoimen luokituksen osalta mediaani on normaalisti edullinen keskiarvon suhteen.