Tähän liittyen yhdistelmän tapauksessa järjestys ei ole lainkaan merkitystä. Ei vain matematiikassa vaan myös käytännön elämässä, käymme näiden kahden käsitteen läpi säännöllisesti. Vaikka emme koskaan huomaa sitä. Joten, lue artikkeli huolellisesti, tietää, miten nämä kaksi käsitettä ovat erilaisia.
Vertailukaavio
| Vertailun perusteet | vaihtelu | Yhdistelmä |
|---|---|---|
| merkitys | Permutaatio tarkoittaa eri tapoja järjestää joukko esineitä peräkkäisessä järjestyksessä. | Yhdistelmällä tarkoitetaan useita tapoja valita kohteita suuresta joukosta esineitä siten, että niiden järjestys ei ole tärkeää. |
| Tilata | merkityksellinen | merkityksetön |
| tarkoittaa | Järjestely | Valinta |
| Mikä se on? | Tilatut elementit | Järjestämättömät sarjat |
| vastaukset | Kuinka monta eri järjestelyä voidaan luoda tietystä objektiryhmästä? | Kuinka monta eri ryhmää voidaan valita suuremmasta ryhmästä? |
| Johtaminen | Useita permutaatioita yhdestä yhdistelmästä. | Yksittäinen yhdistelmä yhdestä permutaatiosta. |
Määritelmä Permutation
Määritämme permutaation erilaisiksi tavoiksi järjestää joitakin tai kaikkia ryhmän jäseniä tietyssä järjestyksessä. Se merkitsee kaiken mahdollisen järjestelyn tai järjestelyn uudelleenjärjestelyn erottuvaan järjestykseen.
Esimerkiksi kaikki mahdolliset permutaatiot, jotka on luotu kirjaimilla x, y, z -
- Ottamalla kaikki kolme kerrallaan ovat xyz, xzy, yxz, yzx, zxy, zyx.
- Ottaen kaksi kerrallaan ovat xy, xz, yx, yz, zx, zy.
N-asioiden mahdollisten permutaatioiden kokonaismäärä, jotka otetaan r kerrallaan, voidaan laskea seuraavasti:
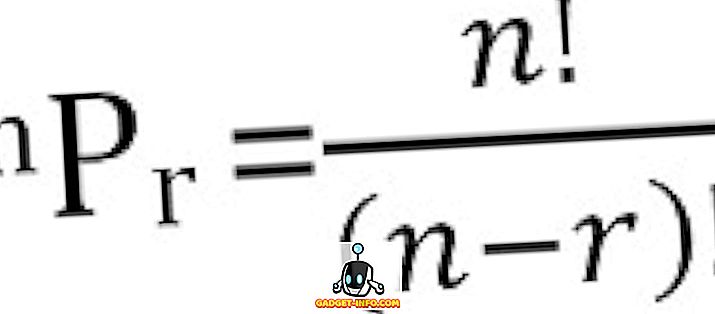
Yhdistelmän määritelmä
Yhdistelmä on määritelty eri tavoin, ryhmän valinnasta ottamalla joukko tai kaikki ryhmän jäsenet ilman seuraavaa järjestystä.
Esimerkiksi kaikki mahdolliset yhdistelmät, jotka on valittu kirjaimella m, n, o -
- Kun kolme valitaan kolmesta kirjaimesta, ainoa yhdistelmä on mno
- Kun valitaan kaksi kolmesta kirjaimesta, mahdolliset yhdistelmät ovat mn, no, om.
N kerrallaan otettujen n-asioiden mahdollisten yhdistelmien kokonaismäärä voidaan laskea seuraavasti:
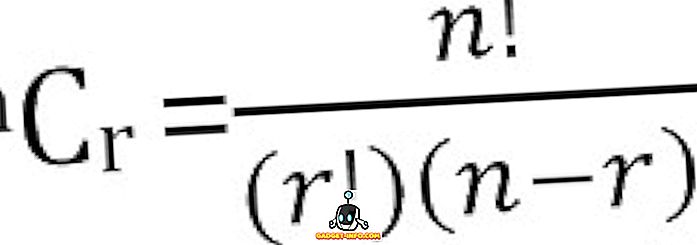
Keskeiset erot Permutation ja Combination välillä
Permutaation ja yhdistelmän erot erotetaan selkeästi seuraavista syistä:
- Termi permutaatio tarkoittaa useita tapoja järjestää joukko esineitä peräkkäisessä järjestyksessä. Yhdistelmä merkitsee useita tapoja valita kohteita suuresta esineiden joukosta siten, että niiden järjestys on merkityksetön.
- Näiden kahden matemaattisen käsitteen ensisijainen erottelupiste on järjestys, sijoittelu ja sijainti, ts. Edellä mainituissa permutaatio-ominaisuuksissa on merkitystä, mikä ei ole merkitystä yhdistelmän tapauksessa.
- Permutaatio tarkoittaa useita tapoja järjestää asioita, ihmisiä, numeroita, aakkosia, värejä jne. Toisaalta yhdistelmä osoittaa eri tapoja valita valikkokohtia, ruokaa, vaatteita, aiheita jne.
- Permutaatio on vain järjestetty yhdistelmä, kun taas yhdistelmä merkitsee järjestämättömiä sarjoja tai arvojen yhdistämistä tietyissä kriteereissä.
- Monet permutaatiot voidaan johtaa yhdestä yhdistelmästä. Sitä vastoin vain yksi yhdistelmä voidaan saada yhdestä permutaatiosta.
- Permutointivastaukset Kuinka monta eri järjestelyä voidaan luoda tietystä objektiryhmästä? Toisin kuin yhdistelmä, joka selittää kuinka monta eri ryhmää voidaan valita suuremmasta ryhmästä esineitä?
esimerkki
Oletetaan, että on olemassa tilanne, jossa sinun täytyy selvittää mahdollisten kahden näytteen joukko kolmesta kolmesta esineestä A, B, C. Tässä kysymyksessä on ensinnäkin ymmärrettävä, onko kysymys permutaatiosta tai yhdistelmä ja ainoa tapa löytää tämä on tarkistaa, onko järjestys tärkeä vai ei.
Jos järjestys on merkittävä, kysymys liittyy permutaatioon, ja mahdolliset näytteet ovat, AB, BA, BC, CB, AC, CA. Jos AB eroaa BA: sta, BC eroaa CB: stä ja AC on erilainen CA.
Jos järjestys on merkityksetön, kysymys liittyy yhdistelmään, ja mahdolliset näytteet ovat AB, BC ja CA.
johtopäätös
Edellä mainitulla keskustelulla on selvää, että permutaatio ja yhdistelmä ovat erilaisia termejä, joita käytetään matematiikassa, tilastoissa, tutkimuksessa ja jokapäiväisessä elämässämme. Muistettavaa on näiden kahden käsitteen osalta se, että tietyn objektiryhmän osalta permutaatio on aina suurempi kuin sen yhdistelmä.