Toisin kuin standardipoikkeama on varianssin laskennassa saadun numeerisen arvon neliöjuuri. Monet ihmiset vastustavat näitä kahta matemaattista käsitettä. Tässä artikkelissa pyritään valaistamaan varianssin ja standardipoikkeaman välinen merkittävä ero.
Vertailukaavio
| Vertailun perusteet | vaihtelu | Normaali poikkeama |
|---|---|---|
| merkitys | Varianssi on numeerinen arvo, joka kuvaa havaintojen vaihtelua sen aritmeettisesta keskiarvosta. | Standardipoikkeama on mittaus, jossa havaintojen jakautuminen tietokokonaisuudessa on. |
| Mikä se on? | Se on neliön poikkeamien keskiarvo. | Se on neliön keskihajonta. |
| Merkitty nimellä | Sigma-neliö (σ ^ 2) | Sigma (σ) |
| Ilmaistuna | Neliöyksiköt | Samat yksiköt kuin tietoryhmän arvot. |
| osoittaa | Kuinka pitkälle ryhmän yksilöt ovat levinneet. | Kuinka paljon havainnot havainnot tietokannasta poikkeavat sen keskiarvosta. |
Varianssin määritelmä
Tilastoissa varianssi määritellään vaihtelevuuden mittarina, joka edustaa, kuinka pitkälle ryhmän jäsenet ovat levinneet. Se selvittää keskimääräisen asteen, jolla jokainen havainto vaihtelee keskiarvosta. Kun datasarjan varianssi on pieni, se osoittaa datapisteiden läheisyyden keskiarvoon nähden, kun taas suurempi varianssiarvo edustaa sitä, että havainnot ovat hyvin hajautuneet aritmeettisen keskiarvon ja toisistaan.
Luokittelemattomat tiedot :
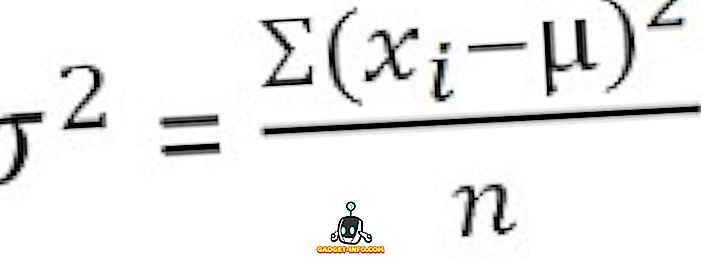
Ryhmitetylle taajuusjakaumalle :
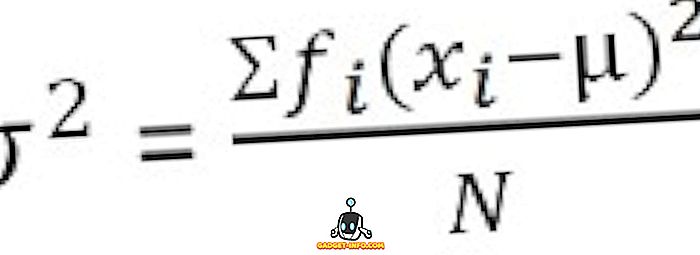
Standardipoikkeaman määrittely
Standardipoikkeama on mitta, jossa kvantifioidaan havaintojen hajaantuminen tietokantaan. Alhainen keskihajonta on osoitus pisteiden läheisyydestä aritmeettiseen keskiarvoon ja korkea standardipoikkeama; tulokset on hajallaan korkeampien arvojen välillä.
Luokittelemattomat tiedot :

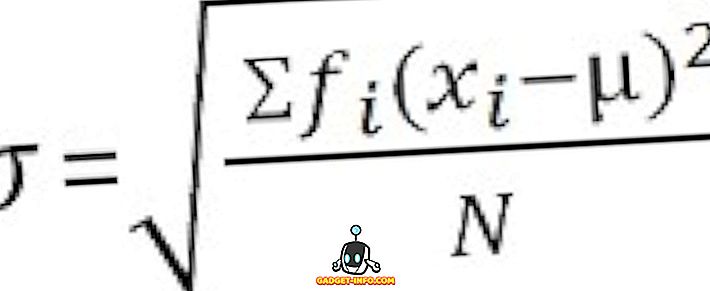
Varianssin ja standardipoikkeaman keskeiset erot
Standardipoikkeaman ja varianssin välinen ero voidaan tehdä selvästi seuraavista syistä:
- Varianssi on numeerinen arvo, joka kuvaa havaintojen vaihtelua sen aritmeettisesta keskiarvosta. Standardipoikkeama on mittaus, jossa havaintojen jakautuminen tietokokonaisuudessa on.
- Varianssi on vain neliön poikkeamien keskiarvo. Toisaalta standardipoikkeama on keskimääräinen neliöpoikkeama.
- Varianssilla merkitään sigma-neliö (σ2), kun taas standardipoikkeama on merkitty sigmaksi (σ).
- Varianssi ilmaistaan neliöyksiköinä, jotka ovat tavallisesti suurempia kuin annetussa tietokannassa olevat arvot. Toisin kuin standardipoikkeama, joka ilmaistaan samoissa yksiköissä kuin tietoryhmän arvot.
- Varianssi mittaa, kuinka pitkälle ryhmät ovat levinneet. Toisaalta, standardipoikkeama mittaa, kuinka paljon havaintojen havainnot tietosarjassa eroavat sen keskiarvosta.
Kuva
Opiskelijan saamat arvot viidestä oppiaineesta ovat 60, 75, 46, 58 ja 80. Sinun täytyy selvittää keskihajonta ja varianssi.
Ensinnäkin sinun täytyy selvittää keskiarvo,

Niinpä keskiarvomerkit ovat 63, 8
Laske nyt varianssi
| X | (XA) | (XA) ^ 2 | |
|---|---|---|---|
| 60 | 63, 8 | -3, 8 | 14.44 |
| 75 | 63, 8 | 11.2 | 125, 44 |
| 46 | 63, 8 | -17, 8 | 316, 84 |
| 58 | 63, 8 | 5.8 | 33.64 |
| 80 | 63, 8 | 16.2 | 262, 44 |
Missä, X = havainnot
A = aritmeettinen keskiarvo
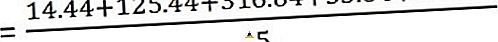
Ja standardipoikkeama on -

yhtäläisyyksiä
- Sekä varianssi että keskihajonta ovat aina positiivisia.
- Jos kaikki havainnot dataryhmässä ovat identtiset, standardipoikkeama ja varianssi ovat nolla.
johtopäätös
Nämä kaksi ovat perustilastoja, joilla on keskeinen rooli eri aloilla. Standardipoikkeama on suositeltavampi kuin keskiarvo, koska se ilmaistaan samoissa yksiköissä kuin mittaukset, kun taas varianssi ilmaistaan yksiköissä, jotka ovat suurempia kuin annetut tiedot.