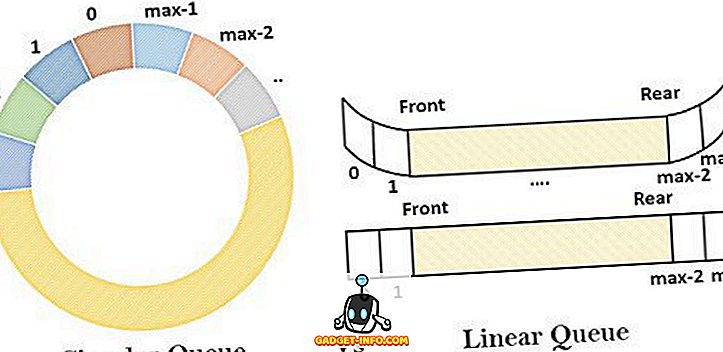
Jonossa voidaan kuvata, että ei-primitiivinen lineaarinen datarakenne seuraa FIFO-järjestystä, jossa dataelementit lisätään yhdestä päästä (takapää) ja poistetaan toisesta päästä (etupää). Muita jonon muunnelmia ovat pyöreä jono, kaksinkertaisesti päättynyt jono ja prioriteettijono.
Vertailukaavio
| Vertailun perusteet | Lineaarinen jono | Pyöreä jono |
|---|---|---|
| perustiedot | Järjestää dataelementit ja ohjeet peräkkäin järjestyksessä. | Järjestää tiedot pyöreään kuvioon, jossa viimeinen elementti on liitetty ensimmäiseen elementtiin. |
| Tehtävän suorittamisen järjestys | Tehtävät suoritetaan ennen niiden sijoittamista (FIFO). | Tehtävän suoritusjärjestys voi muuttua. |
| Lisäys ja poistaminen | Uusi elementti lisätään takaosasta ja poistetaan edestä. | Lisäys ja poistaminen voidaan tehdä missä tahansa asennossa. |
| Esitys | tehoton | Toimii paremmin kuin lineaarinen jono. |
Lineaarisen jonon määritelmä
Lineaarinen jono on rationaalisesti ensimmäinen ensimmäisessä järjestyksessä. Se on ns. Lineaarinen, koska se muistuttaa suoraa viivaa, jossa elementit on sijoitettu yksi toisensa jälkeen. Se sisältää homogeenisen kokoelman elementeistä, joihin lisätään uusia elementtejä toisesta päästä ja poistetaan toisesta päästä. Jonon käsite voidaan ymmärtää esimerkkinä siitä, että yleisö odottaa lippuluettelon ulkopuolella teatterilippua. Tässä jonossa henkilö liittyy jonon takapäähän ottamaan lipun ja lippu annetaan jonon etupäässä.
Jonossa on useita toimintoja
- Ensinnäkin jono alustetaan nollaan (eli tyhjä).
- Määritä, onko jono tyhjä vai ei.
- Määritä, onko jono täynnä vai ei.
- Uuden elementin asettaminen takapäästä (Enqueue).
- Elementin poistaminen etupäästä (Dequeue).
Jono voidaan toteuttaa kahdella tavalla
- Staattisesti (taulukoiden käyttäminen)
- Dynaamisesti (osoittimien käyttäminen)
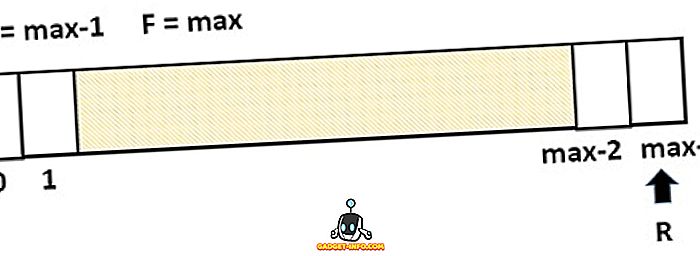
Lineaarisen jonon rajoittaminen on, että se luo skenaarion, jossa yhtään uutta elementtiä ei voi lisätä jonoon, vaikka jonossa on tyhjät välit. Tämä edellä mainittu tilanne on esitetty alla olevassa kuvassa. Täällä takana on viimeinen indeksi, kun taas kaikki laatikot ovat tyhjiä, uusia elementtejä ei voi lisätä.
Pyöreän jonon määritelmä
Pyöreä jono on lineaarisen jonon muunnos, joka tehokkaasti ratkaisee lineaarijonon rajoituksen. Pyöreässä jonossa uusi elementti lisätään jonon ensimmäiseen paikkaan, jos viimeinen on varattu ja tila on käytettävissä. Lineaarisen jonon kohdalla lisäys voidaan suorittaa vain takapäästä ja poistaminen etupäästä. Täydellisessä jonossa peräkkäisten poistojen suorittamisen jälkeen jonossa syntyy tietty tilanne, jossa uutta elementtiä ei voi lisätä vielä, vaikka käytettävissä oleva tila olisi alavirtaustilan (takana = max - 1) edelleen olemassa.
Pyöreä jono yhdistää molemmat päät osoittimen kautta, jossa ensimmäinen elementti tulee viimeisen elementin jälkeen. Se seuraa myös etu- ja takaosaa ottamalla käyttöön ylimääräistä logiikkaa, jotta se voisi jäljittää lisättävät ja poistettavat elementit. Tämän avulla pyöreä jono ei generoi ylivuototilaa, ennen kuin jono on täynnä todellisuudessa.
Joitakin ehtoja, joita seuraa pyöreä jono:
- Edessä on osoitettava ensimmäinen elementti.
- Jono on tyhjä, jos etuosa = takana.
- Kun uusi elementti lisätään, jonoa lisätään arvolla yksi (takana = takana + 1).
- Kun elementti poistetaan jonosta, etuosaa lisätään yhdellä (etu = etu + 1).
Lineaarisen jonon ja pyöreän jonon keskeiset erot
- Lineaarinen jono on järjestetty lista, jossa dataelementit järjestetään peräkkäisessä järjestyksessä. Sitä vastoin pyöreä jono tallentaa tiedot pyöreällä tavalla.
- Lineaarinen jono seuraa FIFO-järjestystä tehtävän suorittamiseksi (ensimmäiseen kohtaan lisätty elementti poistetaan ensimmäisestä sijainnista). Sitä vastoin pyöreässä jonossa elementille suoritettujen toimintojen järjestys voi muuttua.
- Elementtien asettaminen ja poistaminen on kiinteä linjassa, toisin sanoen lisäys takapäästä ja poistaminen etupäästä. Toisaalta pyöreä jono pystyy lisäämään ja poistamaan elementin mistä tahansa pisteestä, kunnes se on tyhjä.
- Lineaarinen jono tuhlaa muistitilaa ja pyöreä jono tehostaa tilan käyttöä.
Lineaarisen jonon toteutus
Alla oleva algoritmi havainnollistaa jonossa olevien elementtien lisäämistä:
Jonossa on kolme datamuuttujaa, joista yksi sisältää jonon tallennuksen ja muut etupuolen ja takapääasennon tallentamiseksi, joka on -1.
lisää (kohta, jono, n, takana) {jos (takana == n) sitten tulosta "jonon ylivuoto"; muu {takana = takana + 1; jono [takana] = kohde; }} Alla oleva algoritmi havainnollistaa jonojen poistamista jonosta:
delete_circular (kohde, jono, takana, edessä) {jos (takana == etu) ja tulosta sitten "jonon alavirta"; muu {front = front + 1; item = jono [edessä]; }} Pyöreän jonon toteutus
Algoritmi, jolla tulkitaan elementin lisäys pyöreässä jonossa:
insert_circular (item, jono, takana, edessä) {takana = (takana + 1) mod n; jos (edessä == takana) tulostetaan "jono on täynnä"; muu {jono [takana] = kohde; }} Algoritmi selittää elementin poistamisen pyöreässä jonossa:
delete_circular (kohde, jono, takana, edessä) {jos (edessä == takana) ja tulosta ("jono on tyhjä"); muu {front = front + 1; item = jono [edessä]; }} johtopäätös
Lineaarinen jono on tehoton tietyissä tapauksissa, joissa elementtien on siirryttävä vapaisiin tiloihin insertiotoiminnon suorittamiseksi. Siksi se pyrkii tuhlaamaan tallennustilaa, kun taas pyöreä jono käyttää asianmukaisesti tallennustilaa, kun elementit lisätään mihin tahansa paikkaan, jos on tyhjä tila.